Intuitive Interpretation of Unexpected Binomial Coefficients

This post will give an intuitive interpretation of the presence of the combination formula (which equals the binomial coefficient) in math problem solutions and probability distributions that are seemingly unrelated to combinations. For example, the binomial coefficient shows up in the probability mass function of the binomial distribution and the negative binomial distribution.

Wikipedia has the following definition for combination:

In mathematics a combination is a way of selecting several things out of a larger group, where (unlike permutations) order does not matter. In smaller cases it is possible to count the number of combinations. For example given three fruit, an apple, orange and pear say, there are three combinations of two that can be drawn from this set: an apple and a pear; an apple and an orange; or a pear and an orange. More formally a k–combination of a set S is a subset of k distinct elements of S. If the set has n elements the number of k-combinations is equal to the binomial coefficient

The binomial coefficient indexed by n and k is denoted . The formula below, for evaluating binomial coefficients, uses factorials.

Now let’s consider the following problem.

Suppose you have a collection of n marbles, of which x are red and y are blue. How many distinguishable ways can the red and blue marbles be ordered in a lineup of marbles? The red marbles are indistinguishable and the blue marbles are also indistinguishable.

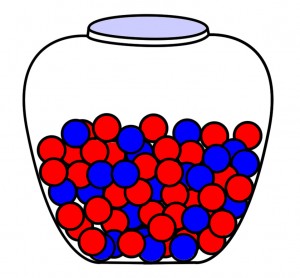This type of problem shows up in many areas. Although the problem I specified uses marbles, the same type of problem could use letters or numbers. For example, I could have asked how many words can be formed with specified amounts of the letters X and O, or how many binary numbers can be written using specified amounts of the digits 1 and 0.

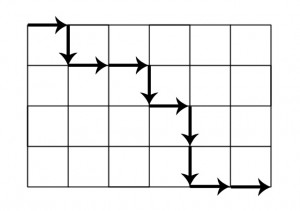
Additionally, I have encountered a similar problem that asks how many ways a grid can be traversed from the top-left corner to the bottom-right corner, with the possibility of moving in only two directions, right or down. Considering that all traversals will have the same number of moves in each of the allowed directions, this problem is analogous to the problem specified above, as the answer can be derived by calculating the number of ways to order the moves. In the picture below, there must be four moves in the down (D) direction and six moves in the right (R) direction. To calculate the number of possible ways to traverse the grid, we can calculate the number of ways to arrange the letters D and R, where there are four Ds and six Rs.

Lastly, the binomial coefficient also shows up in the probability mass function of the binomial distribution (see my prior post—which included a probability distributions reference table—for more details on the binomial distribution). Without getting into too many details, the presence of the term is analogous to the examples above. Basically, if p is the probability of an event succeeding, and q = 1-p is the probability of an event failing, then the probability of an event succeeding k times in n trials, is equal to  multiplied by the number of different ways of distributing the k successes and (n-k) failures, which I like to view as the number of ways that the letters p and q can be arranged.

To solve the marble problem specified above, and those that are similar, I have always first thought about the total number of arrangements of all of the elements. In the case of the marbles, there are n! ways to arrange n objects. However, since there are x red marbles whose ordering is indistinguishable and y blue marbles whose ordering is indistinguishable, the total amount of those orderings (calculated as if the marbles were in fact distinguishable) has to be divided out. The solution to the problem is below.

Since x = n-y and y=n-x, the equation above can be rewritten in the following ways.

If that formula looks familiar, it is the same formula stated above for calculating binomial coefficients (the letters used to index have changed, but the formula remains the same). As you might have noticed, the marble problem didn’t mention anything about combinations, so you may be wondering why the same formula for calculating combinations is used to solve a problem that is seemingly unrelated to combinations.

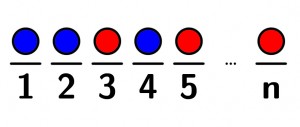
The answer lies in the way that we think about the problem. Instead of only thinking about the number of different ways that we can order the marbles, let’s think about the different places that we’ll put the marbles in a lineup, and give each place a number (or letter, or some other position identifier). Since there are n total marbles, we know that there must be n total places in the lineup.

We know that there will be x places with a red marble and y places with a blue marble. For the blue marbles, we can now ask, of the n places, how many ways can a combination of y places be chosen to put the blue marbles. In the image above, place 1, place 2, place 4, … is one combination of places to put the blue marbles. There are  combinations of y places out of n. Similarly, for the red marbles, we can now ask, of the n places, how many ways can a combination of x places be chosen to put the red marbles. In the image above, place 3, place 5, …, and place n is one combination of places to put the red marbles. There are  combinations of y places out of n.